Исследование знаков синуса, косинуса, тангенса и котангенса по четвертям: ключевые моменты

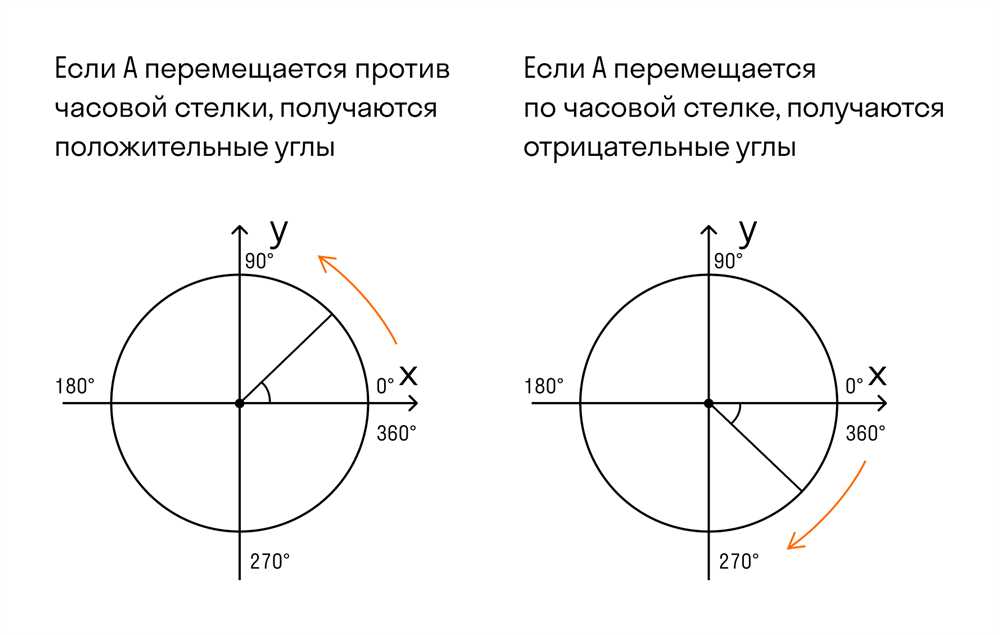
Синус, косинус, тангенс и котангенс - основные тригонометрические функции, которые широко используются в математике, физике, инженерии и других областях науки. Изучение знаков этих функций по четвертям играет важную роль в понимании поведения углов и их функций на плоскости. В этой статье мы рассмотрим, как меняются знаки синуса, косинуса, тангенса и котангенса в каждой из четвертей плоскости.

Четверть I (0° ≤ θ ≤ 90°):

В первой четверти все тригонометрические функции синус, косинус, тангенс и котангенс положительны. Это происходит потому, что в этой области углы находятся между 0° и 90°, где значения функций углов остаются положительными.

Четверть II (90° ≤ θ ≤ 180°):

Во второй четверти только синус является положительным, а косинус, тангенс и котангенс отрицательны. Это связано с тем, что вторая четверть находится между 90° и 180°, где углы больше 90°, а синус - это значение y-координаты, которая остается положительной, в то время как косинус, тангенс и котангенс - это значения x-координаты, которые становятся отрицательными.

Четверть III (180° ≤ θ ≤ 270°):

В третьей четверти только тангенс является положительным, а синус, косинус и котангенс отрицательны. В этой области углы находятся между 180° и 270°, где значения тангенса, определяемые как отношение синуса к косинусу, остаются положительными.

Четверть IV (270° ≤ θ ≤ 360°):

В четвертой четверти только косинус является положительным, а синус, тангенс и котангенс отрицательны. Это происходит потому, что в этой области углы находятся между 270° и 360°, где значения косинуса, определяемые как отношение x-координаты к радиусу, остаются положительными.

Изучение этих знаков помогает понять поведение углов и их тригонометрических функций на плоскости, что является важным аспектом во многих областях науки и техники.